Función Cuadrática
Ejercicios 2 y 12 Función Cuadrática.
Ejercicio 1 de Aplicación/ Función Cuadrática.
Una función cuadrática es aquella que puede escribirse como una ecuación de la forma:
donde a , b y c (llamados términos ) son números reales cualesquiera y a es distinto de cero (puede ser mayor o menor que cero, pero no igual que cero). El valor de b y de c sí puede ser cero .
En la ecuación cuadrática cada uno de sus términos tiene un nombre.
Así,
ax2 es el término cuadrático
bx es el término lineal
c es el término independiente
Cuando estudiamos la ecuación de segundo grado o cuadrática vimos que si la ecuación tiene todos los términos se dice que es una ecuación completa , si a la ecuación le falta el término lineal o el independiente se dice que la ecuación es incompleta.
1. Ejemplo
Nos dan la siguiente función,
Pasos para resolver una función cuadrática
1. Sentido
La gráfica es una parábola.
La orientación de la parábola depende del signo a:
Como a es positivo la parábola va hacia arriba U
a>0 la parábola va hacia arriba.
a<0 la parábola va hacia abajo.
2. Eje de simetría
Dado por la recta
3.Vertice
El vértice es el punto de corte con el eje de abscisas remplazamos el resultado que nos dio en el eje de simetría (x) en la función dada.
4.Interceptos
Los puntos de corte con el eje de abscisas vienen dados por la solución
Reemplazamos
Y sabemos que el intercepto y: es el valor de c.
Gráficamente
2. Ejemplo
Nos dan la siguiente función,
Pasos para resolver una función cuadrática
1. Sentido
La gráfica es una parábola.
La orientación de la parábola depende del signo a:
Como a es positivo la parábola va hacia arriba U
a>0 la parábola va hacia arriba.
a<0 la parábola va hacia abajo.
2. Eje de simetría
Dado por la recta
3.Vertice
El vértice es el punto de corte con el eje de abscisas remplazamos el resultado que nos dio en el eje de simetría (x) en la función dada.
4.Interceptos
Los puntos de corte con el eje de abscisas vienen dados por la solución
La determinante no puede ser negativa, así que tabulamos para darle otro valor a x.
En este caso reemplazamos x=1
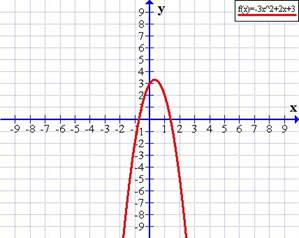
Gráficamente
Problema de aplicación
1. Sentido
3.Vertice
4.interceptos
2. Eje de simetría
No hay comentarios:
Publicar un comentario